Are you finding yourself lost in the ocean of sine, cosine, and tangent? Do those trigonometric identities feel like an alien language? Fear not! With a structured approach, a little practice, and some clever techniques for memorization, mastering trigonometry formulas for your class 10, 11, and 12 exams can be easy and fun. This comprehensive guide aims to make these formulas stick with you and equip you with the necessary tools to ace your board exams.
Why Trigonometry Matters?
Before diving into formulas, let’s address the elephant in the room: “Why do I need to learn this?” Besides the obvious answer of “to pass your board exams,” trigonometry has practical applications everywhere:
- Architecture and construction (calculating heights, and angles of roofs)
- Navigation (GPS systems)
- Music theory (sound waves)
- Physics (optics, mechanics, electricity)
- Computer graphics and game design
The patterns and relationships in trigonometry appear throughout nature and technology. Mastering these concepts opens doors to understanding how our world works—and yes, it will help you ace those board exams!
Introduction to Trigonometry: What’s All the Fuss About?
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, primarily focusing on right-angled triangles. It helps us understand the world around us in a new light – from engineering and physics to architecture and even computer graphics.
In trigonometry, we work with trigonometric ratios – functions like sine (sin), cosine (cos), and tangent (tan) that are directly related to the sides of a right-angled triangle. Mastery of these formulas is crucial for solving problems on your board exams, and the more efficiently you recall them, the better you will perform.
Trigonometry Formula for Class 10 – Building the Foundation
Before diving into complex identities and theorems, let’s ensure we have a solid foundation of all the formulas you’ll encounter. The ratios are based on a right-angled triangle:
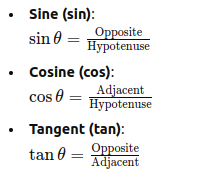
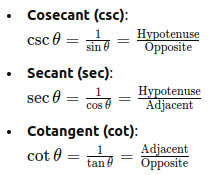
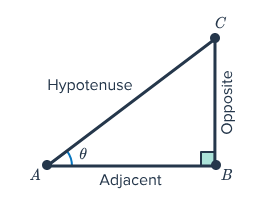

Memory Aid 1: "SOHCAHTOA"
The classic mnemonic for the primary ratios:
- Sin = Opposite / Hypotenuse
- Cos = Adjacent / Hypotenuse
- Tan = Opposite / Adjacent
Memory Aid 2: "Some People Have Curly Brown Hair Turn Permanently Black”
An extended mnemonic for all six ratios: let us call ‘Adjacent’ to be “Base” and ‘Opposite’ to be “Perpendicular” to understand the trick.
- Sin = Perpendicular / Hypotenuse
- Cos = Base / Hypotenuse
- Tan = Perpendicular / Base
- Cosec = 1/Sin = Hypotenuse / Perpendicular
- Sec =1/Cos = Hypotenuse / Base
Cot = 1/tan = Base / Perpendicular
Standard Angles and Their Values
Knowing these values by heart is non-negotiable for board exam success:
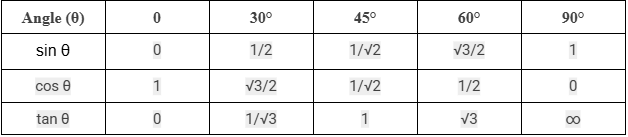
Memory Aid 3: "The Dance of Square Roots"
- For sine values (0° to 90°): 0, 1/2, 1/√2, √3/2, 1
- Notice the pattern: 0, 1/2, then the square roots dance in: 1/√2, √3/2, 1
- For cosine values (0° to 90°): 1, √3/2, 1/√2, 1/2, 0
It’s just sine in reverse!
Memory Aid 4: "The Fraction Race"
Imagine the fractions as runners in a race:
- Sin starts at 0 and finishes at 1
- Cos starts at 1 and finishes at 0
- As sin increases, cos decreases
Fundamental Identities:
Pythagorean Identities
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = cosec²θ
Memory Aid 5: "The Square Circle Dance"
- Picture sine and cosine dancing in a unit circle: “Sine squared plus cosine squared makes a perfect circle of radius one!”
- For the other identities: “Add the square of the ratio to 1, and you get the square of its reciprocal!”
Complementary Angle Relationships
For any angle θ:
- sin(90° – θ) = cos θ
- cos(90° – θ) = sin θ
- tan(90° – θ) = cot θ
Trigonometry Formula for Class 11 & 12 – Advanced Concepts
Quadrant Rules: Signs Matter!
Understanding where functions are positive or negative is crucial:
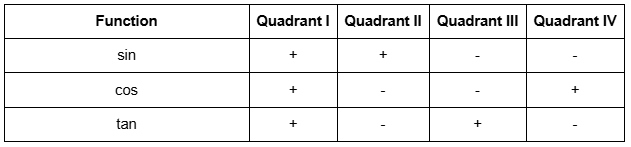
Memory Aid 6: "All Students Take Calculus"
To remember where functions are positive:
- All functions are positive in Quadrant I
- Sine (and cosecant) are positive in Quadrant II
- Tangent (and cotangent) are positive in Quadrant III
- Cosine (and secant) are positive in Quadrant IV
Memory Aid 7: "Co-Functions are Complements"
The prefix “co-” in cosine, cotangent, and cosecant is the clue! “Co-” functions are related to complementary angles (angles that add up to 90°).
Negative Angle Identities
- sin(-θ) = -sin θ
- cos(-θ) = cos θ
- tan(-θ) = -tan θ
Memory Aid 8: "Cosine is Even, Others are Odd"
- Cosine is even-tempered (doesn’t change sign with negative angles)
- Sine and tangent are odd-tempered (change signs with negative angles)
- This pattern extends to their reciprocals (secant is even, cosecant and cotangent are odd)
Identities: Level Up for Class 11 and 12
Sum and Difference Formulas
For angles α and β:
Sin of Sum/Difference:
⦁ sin(α + β) = sin α cos β + cos α sin β
⦁ sin(α – β) = sin α cos β – cos α sin β
Cos of Sum/Difference:
⦁ cos(α + β) = cos α cos β – sin α sin β
⦁ cos(α – β) = cos α cos β + sin α sin β
Tan of Sum/Difference:
⦁ tan(α + β) = (tan α + tan β)/(1 – tan α tan β)
⦁ tan(α – β) = (tan α – tan β)/(1 + tan α tan β)
Memory Aid 9: : "SOAP" for Sine of Sum
For sin(α + β):
⦁ Sine of first × coSine of second
⦁ plus
⦁ cosIne of first × sIne of second
For cos(α + β), it’s the same pattern but with a minus instead of plus.
Memory Aid 10:"The Sum-Difference Switch"
Notice how sin and cos sum/difference formulas follow a pattern:
⦁ In sin formulas, the middle sign matches the operation (+ for addition, – for subtraction)
⦁ In cos formulas, the middle sign is opposite to the operation (- for addition, + for subtraction)
Double Angle Formulas
⦁ sin 2θ = 2 sin θ cos θ
⦁ cos 2θ = cos²θ – sin²θ = 2cos²θ – 1 = 1 – 2sin²θ
⦁ tan 2θ = 2tan θ/(1 – tan²θ)
Memory Aid 11: "Double the Angle, Double the Fun"
For sin 2θ, imagine double high-fiving:
⦁ “Two hands slap together” = 2 sin θ cos θ
For cos 2θ, you have three options (pick your favorite):
⦁ “Cosine squared minus sine squared”
⦁ “Twice cosine squared minus one”
⦁ “One minus twice sine squared”
Triple Angle Formulas
⦁ sin 3θ = 3sin θ – 4sin³θ
⦁ cos 3θ = 4cos³θ – 3cos θ
Memory Aid 12: "The Rule of 3-4"
Notice both formulas involve 3 and 4:
⦁ Sin: 3 times first degree minus 4 times third degree
⦁ Cos: 4 times third degree minus 3 times first degree
⦁ Notice the pattern: 3 and 4 appear in both but in opposite orders!
Half-Angle Formulas
⦁ sin(θ/2) = ±√[(1 – cos θ)/2]
⦁ cos(θ/2) = ±√[(1 + cos θ)/2]
⦁ tan(θ/2) = (1 – cos θ)/sin θ = sin θ/(1 + cos θ)
Memory Aid 13: "Product Pattern"
- Same functions (sin×sin or cos×cos) give cosine results.
- Different functions (sin×cos) give sine results.
- For sin×sin: minus sign between terms.
- For cos×cos: plus sign between terms.
- For sin×cos: always plus sign between terms.
Think of the half-angle formulas as finding half of something under a square root:
⦁ Sin half-angle: “One minus cosine, divided by two, all under a radical”
⦁ Cos half-angle: “One plus cosine, divided by two, all under a radical”
Product-to-Sum & Sum-to-Product Formulas
Product-to-Sum Formulas
⦁ sin α sin β = ½[cos(α – β) – cos(α + β)]
⦁ cos α cos β = ½[cos(α – β) + cos(α + β)]
⦁ sin α cos β = ½[sin(α + β) + sin(α – β)]
Memory Aid 14: "Product Pattern"
⦁ Same functions (sin×sin or cos×cos) give cosine results
⦁ Different functions (sin×cos) give sine results
⦁ For sin×sin: minus sign between terms
⦁ For cos×cos: plus sign between terms
⦁ For sin×cos: always plus sign between terms
Memory Aid 15: "Same-Same-Different Rule"
“When same meets same, cosine comes out, When different functions come about, Sine is what it’s all about. Sin-sin takes minus in the middle, Cos-cos takes plus without a riddle, Sin-cos takes plus as clear as a fiddle!”
Sum-to-Product Formulas
⦁ sin α + sin β = 2 sin[(α + β)/2] cos[(α – β)/2]
⦁ sin α – sin β = 2 cos[(α + β)/2] sin[(α – β)/2]
⦁ cos α + cos β = 2 cos[(α + β)/2] cos[(α – β)/2]
⦁ cos α – cos β = -2 sin[(α + β)/2] sin[(α – β)/2]
Memory Aid 16: "The SCCS Pattern"
⦁ Sin plus Sin: Start with Sin, follow with Cos
⦁ Sin minus Sin: Start with Cos, follow with Sin
⦁ Cos plus Cos: Double Cos (both terms are cosine)
⦁ Cos minus Cos: Double Sin with negative sign
Memory Aid 17: "Sum-to-Product Rhyme"
“Sine plus sine: sine-cosine in a line, Sine minus sine: cosine-sine works fine, Cosine plus cosine: cosine twice will shine, Cosine minus cosine: sine twice with a negative sign.”
Advanced Circular Function Relationships
Periodicity Identities
- sin(θ + 2π) = sin θ
- cos(θ + 2π) = cos θ
- tan(θ + π) = tan θ
Memory Aid 18: "The Circle of Life"
“Sine and cosine come full circle after 2π, Tangent only needs π to begin anew!”
Supplementary Angle Relationships
⦁ sin(π – θ) = sin θ
⦁ cos(π – θ) = -cos θ
⦁ tan(π – θ) = -tan θ
Memory Aid 19: "Supplementary Surprise"
“When angles add to make a straight line (π), Sine stays the same, feeling fine, But cosine and tangent change their sign!”
The Connection System
Create logical connections between formulas:
⦁ Double angle formulas are derived from sum formulas (when α = β)
⦁ Half-angle formulas come from double-angle formulas (substitute 2θ = α)
⦁ Triple-angle formulas combine double-angle and sum formulas
Memory Aid 20: "The Formula Family Tree"
Visualize all formulas as members of a family:
⦁ Pythagorean identities are the grandparents
⦁ Sum and difference formulas are the parents
⦁ Double and half-angle formulas are the children
⦁ Triple angle formulas are the cousins
⦁ Product-to-sum and sum-to-product are the siblings
The Visual Association System
Create vivid mental images:
⦁ For sin²θ + cos²θ = 1: Picture a right triangle inside a unit circle
⦁ For double angle formulas: Imagine an angle doubling in size
⦁ For quadrant rules: Visualize a compass with signs marked in each direction
Practice Technique: The Derivation Method
Instead of pure memorization, learn to derive formulas:
⦁ Start with the sum formulas and derive double angle formulas (set α = β)
⦁ Use Pythagorean identities to transform expressions
⦁ Practice deriving one formula from another until it becomes second nature
The "Check Special Values" Technique
If unsure about a formula during the exam:
⦁ Substitute special values (0°, 30°, 45°, 90°)
⦁ Verify both sides of the equation match
⦁ This works especially well for identities you’re unsure about
Memory Aid 21: "The Special Four"
“When in doubt, check it out, With 0, 30, 45, and 90 all about. If both sides match without a doubt, Your formula is correct, no need to pout!”
Common Mistakes to Avoid in Board Exams
⦁ Sign errors: Especially in quadrants II, III, and IV
⦁ Formula confusion: Double-checking which identity to apply
⦁ Degree/radian mix-ups: Being consistent with your angle measures
⦁ Algebraic slips: Taking care with simplifications
Memory Aid 22: "SAFE Exam Technique"
⦁ Signs (be careful with negative signs)
⦁ Angle measures (be consistent with degrees/radians)
⦁ Formulas (double-check which one applies)
⦁ Equation solving (watch your algebra steps)
Test-Taking Strategies
⦁ Quick verification- Use special angles (0°, 30°, 45°) to check if your formula is correct
⦁ Draw unit circles- Helps visualize relationships
⦁ Write down formulas first- Before starting the problem
⦁ Cross-check answers- Substitute back to verify
Memory Aid 23: "VDCS"
Verify with special angles, Draw unit circles, Create formula sheets, Substitute back
The Spaced Repetition System
Don’t try to memorize everything at once! Follow this schedule:
⦁ Day 1: Basic ratios and standard angles
⦁ Day 2: Review Day 1 + Pythagorean identities
⦁ Day 3: Review Day 2 briefly + Sum/difference formulas
⦁ Day 4: Review Day 3 briefly + Double angle formulas
⦁ Day 7: Review everything briefly + Product to sum formulas
⦁ Day 10: Comprehensive review
⦁ Day 15: Another comprehensive review
Conclusion: Making Trigonometry Your Friend
Trigonometry isn’t just about passing exams—it’s a powerful mathematical tool that reveals our universe’s elegant patterns. By mastering these formulas through systematic memory techniques, you’re not just memorizing meaningless symbols; you’re gaining access to a language that describes circles, waves, oscillations, and cycles—phenomena that appear everywhere from music to physics, architecture to biology.
The brain loves patterns, stories, and connections. Using the memory aids in this guide, you’re working with your brain’s natural strengths rather than against them. Whether you prefer visual associations, silly stories, or rhythmic mnemonics, find what works for you and stick with it.
If you found this guide helpful, share it with your classmates and drop your questions in the comments below! Need a trigonometry formula cheat sheet? Download it from below!











2 Responses
Thank You for the information, Really liked the blog !
Thanks for the pdf, it was really helpful